| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 브루트포스 알고리즘
- 프로그래머스스쿨
- 문자열
- level2
- 너비 우선 탐색
- 그래프이론
- DFS
- 그래프 탐색
- 다이나믹 프로그래밍
- 그리디 알고리즘
- lv2
- 자료구조
- 스택
- 딕셔너리
- programmers
- BFS
- 구현
- 정렬
- DP
- 자바스크립트
- 웹 프론트엔드
- 파이썬
- 그래프 이론
- web
- BASIC
- JavaScript
- CSS
- 알고리즘
- 백준
- 프로그래머스
- Today
- Total
DevLog:-)
[알고리즘][파이썬]1309-동물원 본문
문제
문제 파악
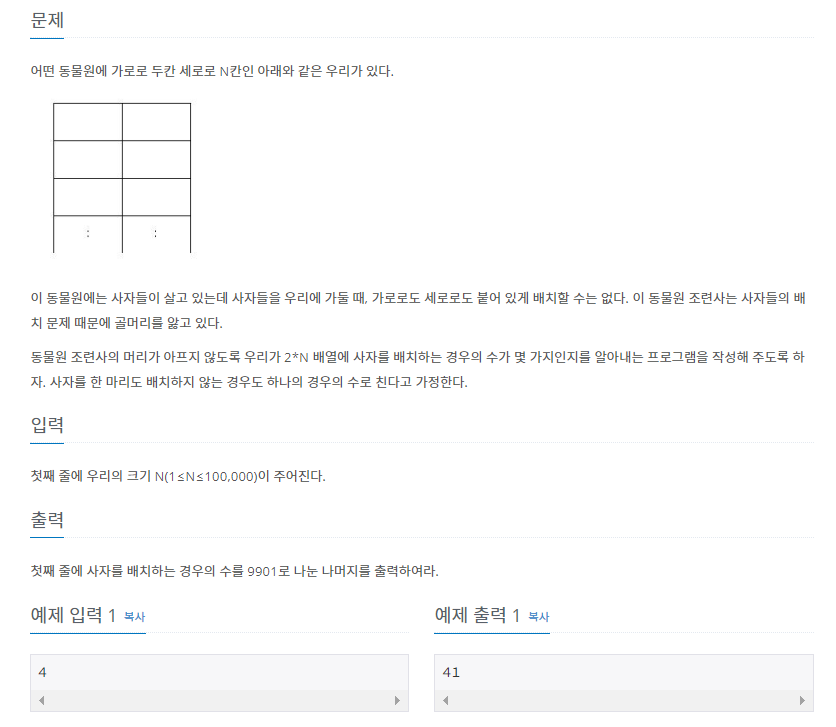
가로 두 칸, 세로 N 칸인 우리에 사자를 배치하는 문제이다.
배치할 때 조건은 가로, 세로로 붙어 있게 배치할 수 없다는 것이다.
N이 커질 수록 이전의 결괏값을 활용해서 풀 수 있는 문제이다. -> DP
규칙을 찾고 점화식을 찾아보자
예제 분석
N이 늘어날 수록 맨 밑에 칸이 추가된다고 생각하면 맨 밑에 칸에 사자를 어떻게 놓을 것이냐에 따라
개수를 찾고 규칙을 찾을 수 있다. 크게 두 가지(놓지 않는 경우, 놓는 경우)로 나눌 수 있다.
N = 1 일때 : 놓지 않는 경우 (1) + 놓는 경우 (2) = 총 3
N = 2 일때 : 놓지 않는 경우 (3) + 놓는 경우 (2+2) = 총 7
N = 3 일때 : 놓지 않는 경우 (7) + 놓는 경우 (5+5) = 총 17
-놓지 않는 경우의 특징 : 놓지 않는 경우는 이전의 칸이 어떻든 상관이 없다.
따라서 N-1일 때 경우의 수와 같다.
-놓는 경우의 특징 : 놓는 경우는 또 두 가지(오른쪽에 놓을지, 왼쪽에 놓을지) 경우로 나눌 수 있다.
오른 쪽에 넣는 경우의 수: 바로 위에 칸에서 왼쪽에 놓였을 때 + 안 놓였을 때
왼쪽에 넣는 경우의 수: 바로 위에 칸에서 오른쪽에 놓였을 때 + 안 놓였을 때
정리하면 규칙이 보인다!
-놓지 않는 경우 : 이전 경우의 수 = dp [N-1]
-놓는 경우 : (이전 경우에서 오른쪽에 놓을 때 + 이전 경우에서 안 놓을 때)
+ (이전 경우에서 왼쪽에 놓을 때 + 이전 경우에서 안 놓을 때)
= { (dp[N-1]-dp [N-2])/2 + dp[N-2] } + { (dp[N-1]-dp[N-2]) /2 + dp[N-2] }
= { (dp[N-1]-dp[N-2])/2 + dp[N-2] } x 2
= 2dp [N-1] - dp [i-2] (최종 점화식)

코드
import sys
N = int(sys.stdin.readline())
dp = [0 for i in range(N+1)]
dp[0] = 1 #N이 2일때 계산을 위해
dp[1] = 3
for i in range(2,N+1):
dp[i] = (dp[i-1]*2 + dp[i-2])%9901
print(dp[N])
'알고리즘 > 백준' 카테고리의 다른 글
| [알고리즘][파이썬]2145-숫자 놀이 (0) | 2023.07.20 |
|---|---|
| [알고리즘][파이썬]2839-설탕 배달 (0) | 2023.07.17 |
| [알고리즘][파이썬]2579-계단오르기 (0) | 2023.07.13 |
| [알고리즘][파이썬]14501-퇴사 (0) | 2023.07.12 |
| [알고리즘][파이썬]1302-베스트 셀러 (0) | 2023.07.10 |




